AVL树

定义

graph LR
    X(性质)

    X --> A("树中任意结点平衡因子(左子树高度 - 右子树高度)绝对值不超过 1")
    X --> B(树中每个左子树和右子树都是 AVL 树)
    X --> C(AVL 树是特殊二叉搜索树)
    X --> D(在平衡因子大于1时会通过旋转来调整树结构, 以重新满足平衡因子不超过1)

graph TB
    A((  ))
    A --> B(( ))
        B --> B2(( ))
        B --> B3(( ))
            B3 --> B4(( ))
    A --> C(( ))
        C --> C1(( ))

标记平衡因子

graph TB
    A((1))
    A --> B(("-1"))
        B --> B2(("0"))
        B --> B3(("1"))
            B3 --> B4(("0"))
    A --> C(("-1"))
        C --> C1(("0"))

该树为$AVL$树

实现

节点定义

template <class T>
typedef struct AVLNode {
    T value;

    int height;
    AVLNode<T> *leftSon;
    AVLNode<T> *rightSon;
    
    AVLNode(T value, AVLNode<T> *leftSon, AVLNode<T> *rightSon, int height){
        this->value = value;
        this->leftSon = leftSon;
        this->rightSon = rightSon;
        this->height = height;
    }
} AVLNode, AVLNodeList;

节点信息

获取节点高度

template <class T>
int GetHeight(AVLNode<T> *node) {
    if(node == nullptr) {
        return 0;
    }
    return node->height;
}

获取节点平衡因子

template <class T>
int GetBalanceFactor(AVLNode<T> *node) {
    if(node == nullptr) {
        return 0;
    }

    return GetHeight(node->leftSon) - GetHeight(node->rightSon);
}

判断

// 判断是否平衡
template <class T>
bool IsBalance(AVLNode<T> *node) {
    if(node == nullptr){
        return true;
    }

    if(abs(GetBalanceFactor(node)) > 1) {
        return false;
    }

    return IsBalance(node->leftSon) && IsBalance(node->rightSon);
}

左旋

$AVL$ 树若在右子树插入右孩子导致失衡时, 单左旋调整
旋转围绕最小失衡子树根节点进行

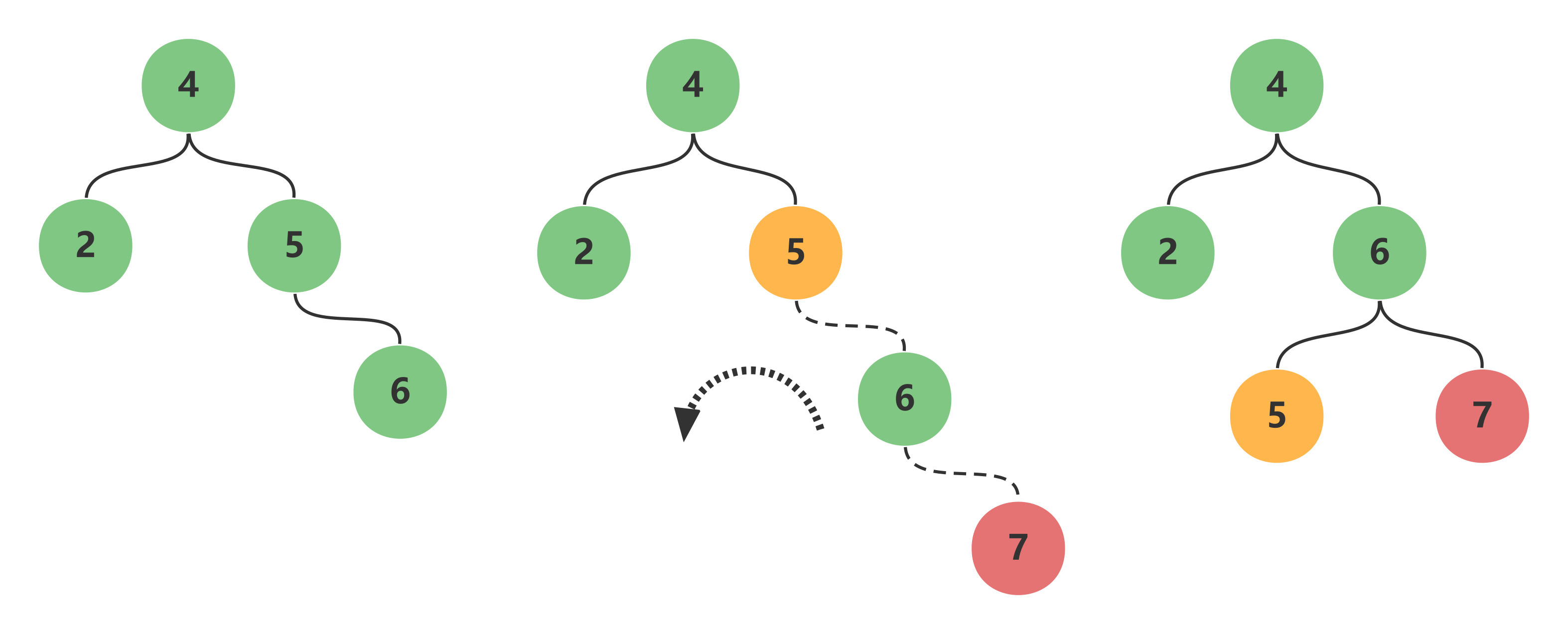
原本平衡$AVL$树插入节点$7$后导致不平衡

最小失衡子树根节点为节点$5$

// 左旋, root为最小失衡子树根节点
template <class T>
AVLNode<T> *LeftRotate(AVLNode<T> *root) {
    AVLNode<T> *p = root->rightSon;

    root->rightSon = p->leftSon;
    p->leftSon = root;

    // 改变指向后, 更新结点对应高度
    root->height = max(GetHeight(root->leftSon), GetHeight(root->rightSon)) + 1;
    p->height = max(GetHeight(p->leftSon), GetHeight(p->rightSon)) + 1;

    return p;
}

右旋

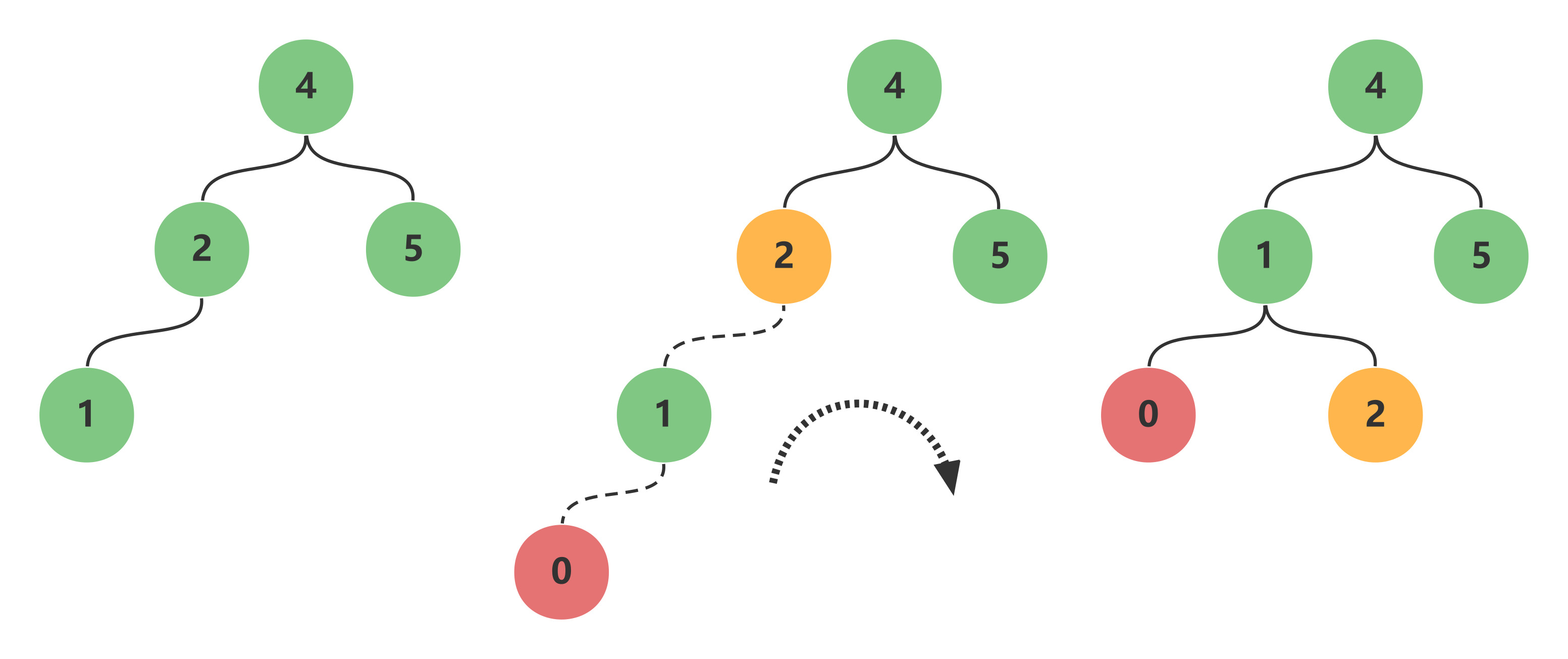
$AVL$ 树若在左子树插入左孩子导致失衡时, 单右旋调整
旋转围绕最小失衡子树根节点进行

template <class T>
AVLNode<T>* RightRotate(AVLNode<T> *&root) {
    AVLNode<T> *p = root->leftSon;

    root->leftSon = p->rightSon;
    p->rightSon = root;

    root->height = max(GetHeight(root->leftSon), GetHeight(root->rightSon)) + 1;
    p->height = max(GetHeight(p->leftSon), GetHeight(p->rightSon)) + 1;
    return p;
}

先右旋后左旋

$AVL$ 树在 右子树上插入左孩子导致失衡时, 先右旋后左旋调整

template <class T>
AVLNode<T>* RightAndLeftRotate(AVLNode<T> *&root) {
    root->rightSon = RightRotate(root->rightSon);
    return LeftRotate(root);
}

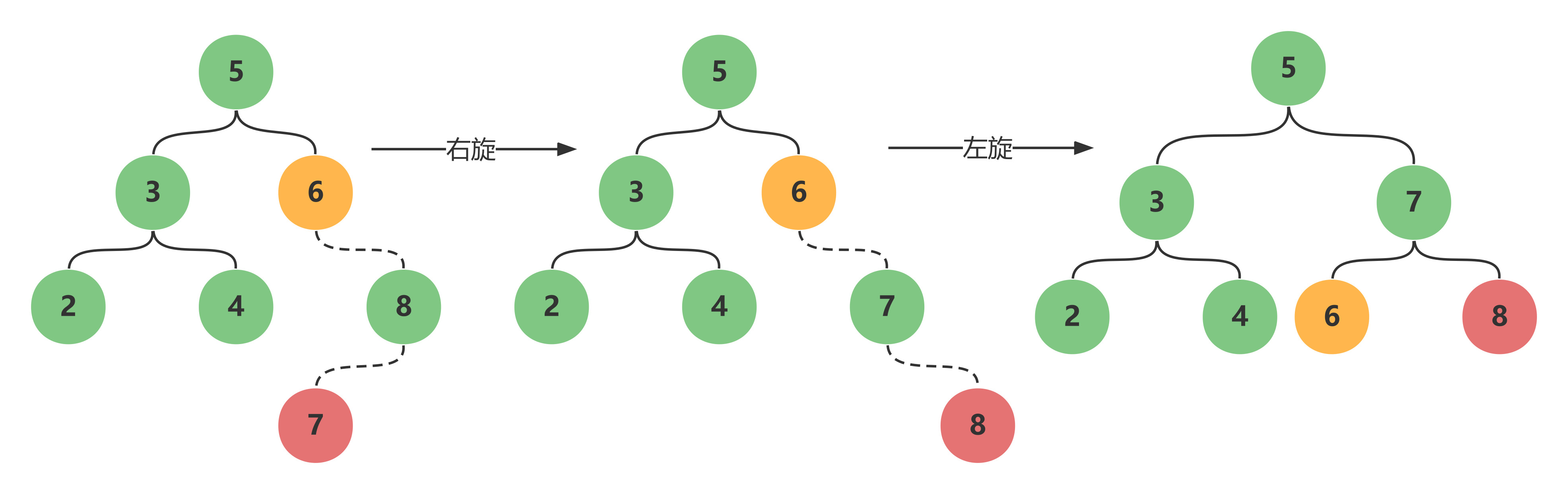
红色为插入节点;绿色为最小失衡子树根节点

先左旋后右旋

$AVL$ 树在左子树上插入右孩子导致失衡时, 先左旋后右旋调整

template <class T>
AVLNode<T>* LeftAndRightRotate(AVLNode<T> *&root) {
    root->leftSon = LeftRotate(root->leftSon);
    return RightRotate(root);
}

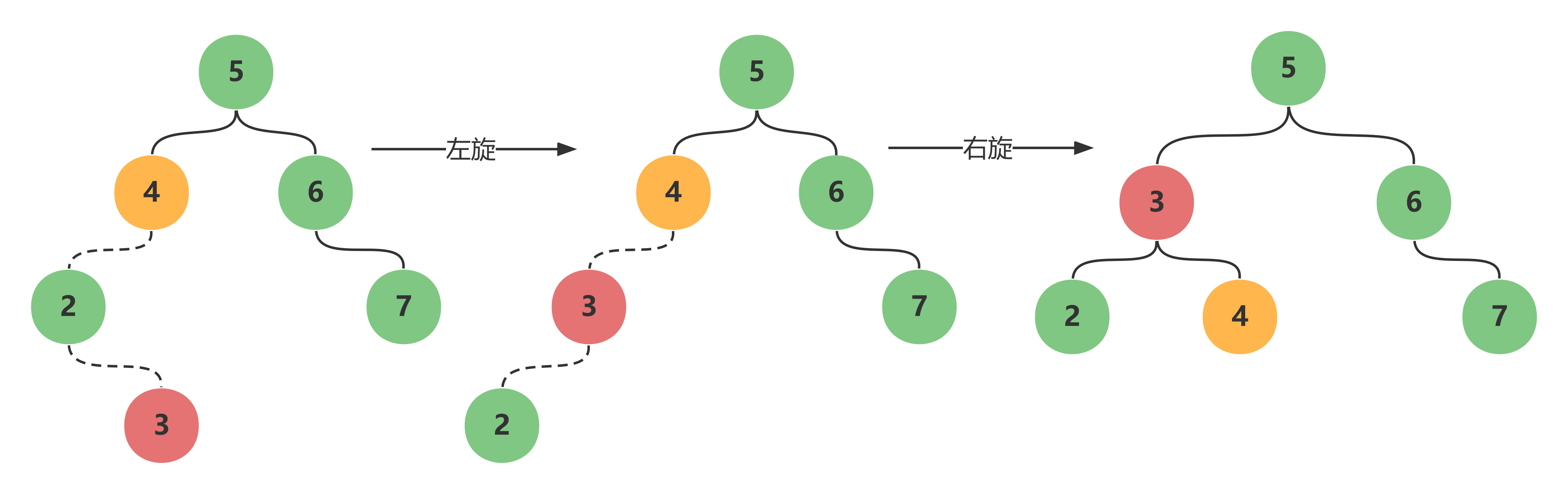
红色为插入节点, 绿色为最小失衡子树根节点

上篇哈夫曼树

下篇线段树