定义
用一颗二叉树来表示线段树,
-
每个节点表示一个区间
-
每个非叶子节点均有左右两颗子树, 对应区间左半与右半部分
给根节点编号 $1$, 对于节点 $i$, 其左节点编号为 $2i$, 右节点编号为 $2i+1$
-
对于任意节点, 表示区间范围为$[l, r]$:
若 $l = r$, 则此为叶子节点
否则令 $mid = \lfloor {\frac{l+r}{2}} \rfloor$, 左儿子对于$[l, mid]$区间, 右儿子对应$[mid+1, r]$区间
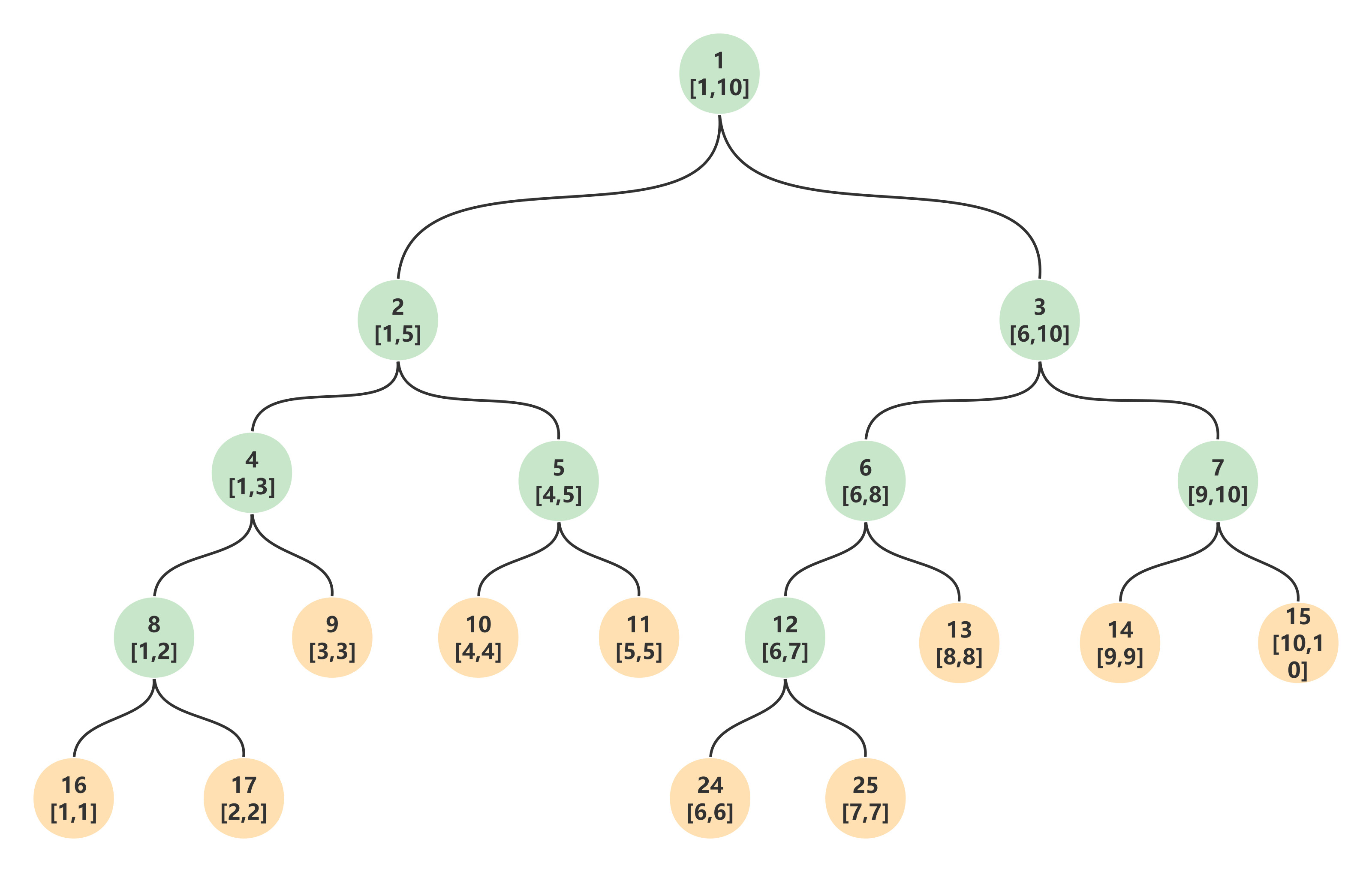
$n = 10$ 时线段树
节点 $1$, 管理范围为$[1, 10]$, 节点 $2$, 管理范围为$[1, 5]$, 节点 $12$, 管理范围为$[6, 7]$
$\cdots$
操作
构建维护
线段树常用来维护区间上某些信息
构建是一个递归过程, 父节点信息需子节点去更新
void Build(int node, int start, int end) {
if (start == end) {
// 叶子节点
mTree[node] = mData[start];
return;
}
int mid = (start + end) / 2;
int leftNode = 2 * node + 1;
int rightNode = 2 * node + 2;
Build(leftNode, start, mid);
Build(rightNode, mid + 1, end);
mTree[node] = Merge(mTree[leftNode], mTree[rightNode]);
}
单点更新
单点更新就是从线段树根节点开始, 一直走到叶子节点, 并更新途径节点值即可
void UpdateNode(int node, int start, int end, int idx, T value) {
if (start == end) {
// 叶子节点更新
mData[idx] = value;
mTree[node] = value;
return;
}
int mid = (start + end) / 2;
int leftNode = 2 * node + 1;
int rightNode = 2 * node + 2;
if (idx <= mid) {
UpdateNode(leftNode, start, mid, idx, value);
} else {
UpdateNode(rightNode, mid + 1, end, idx, value);
}
mTree[node] = Merge(mTree[leftNode], mTree[rightNode]);
}
区间查询
// 查询区间 [left, right] 的值
T QueryRange(int node, int start, int end, int left, int right) {
if (right < start || left > end) {
// 查询范围完全在节点范围之外
return GetIdentity();
}
if (left <= start && end <= right) {
// 查询范围完全包含节点范围
return mTree[node];
}
int mid = (start + end) / 2;
int leftNode = 2 * node + 1;
int rightNode = 2 * node + 2;
T leftResult = QueryRange(leftNode, start, mid, left, right);
T rightResult = QueryRange(rightNode, mid + 1, end, left, right);
return Merge(leftResult, rightResult);
}