质数

朴素算法

• C++

bool IsPrime(int n) {
    if (n & 1 == 0) {
        return false;
    }

    for (int i = 2; i * i < n; i++) {
        if (n % i == 0) {
            return false;
        }
    }
    return true;
}

• python

def is_prime(n: int)-> bool:
    if n & 1 == 0 :
        return False
    if n <= 1 :
        return False
    if n == 2 :
        return True
    for i in range(2, n):
        if n % i == 0:
            return False
    return True

埃拉托斯特尼筛法

从$2$ 开始, 将每个质数的倍数都标记成合数

$2$ 为素数, 则其倍数 $4, 6, 8 \cdots$ 均不是素数

graph TB;
    A2(2):::Style
    A3(3)
    A4(4):::Style
    A5(5)
    A6(6):::Style
    A7(7)
    A8(8):::Style
    A9(9)
    A10(10):::Style

    classDef Style fill:#FFCCFF

$3$ 为素数, 则其倍数 $6, 9, 12 \cdots$ 均不是素数

graph TB;
    A2(2):::Style
    A3(3):::Style
    A4(4):::Style
    A5(5)
    A6(6):::Style
    A7(7)
    A8(8):::Style
    A9(9)
    A10(10):::Style
    
    classDef Style fill:#FFCCFF

$\cdots$

$2~n$ 需要判断 $n-1$ 次

• C++

// 求2-n之间的所有素数
const int n = 100;

// 标记所有数为素数
bool isPrime[n + 1] = { true };

// 存储素数
int prime[n];

int index = 0;

// 所有大于2的偶数均不是素数
for (int i = 4; i <= n; i += 2) {
    isPrime[i] = false;
}

for (int i = 2; i <= n; i++) {
    // 某个奇数为素数
    if (isPrime[i]) {
        prime[index++] = i;
        // 则它的倍数均不是素数
        for (int j = 2 * i; j < n; j += i) {
            isPrime[j] = false;
        }
    }
}

• python

n = 100

is_prime = [True] * (n + 1)

prime = []

for i in range(4, n + 1, 2):
    is_prime[i] = False

for i in range(2, n + 1):
    if is_prime[i]:
        prime.append(i)
        for j in range(2 * i, n, i):
            is_prime[j] = False

欧拉筛

用最小质因子来筛选, 确保每个合数只被筛选一次

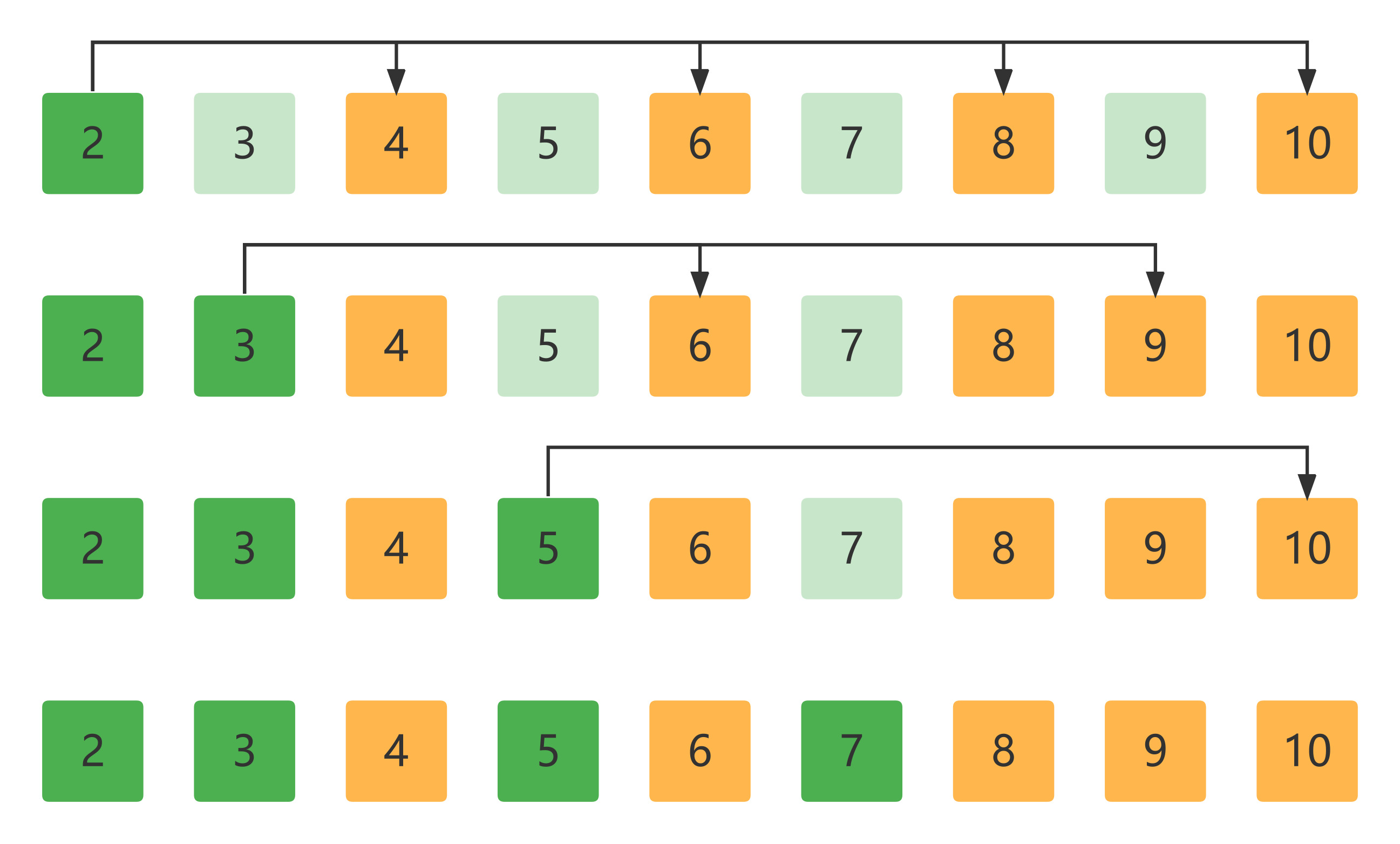
• $i = 2$,

  $j = 0, prime[0] = 2, i * prime[0] = 4$

• $i = 3$,

  $j = 0, prime[0] = 2, i * prime[0] = 6$

  $j = 1, prime[1] = 3, i * prime[1] = 9$

• $i = 4$,

  $j = 0, prime[0] = 2, i * prime[0] = 8$

• $i = 5$,

  $j = 0, prime[0] = 2, i * prime[0] = 10$

• $i = 6, i = 7$

// 求2-n之间的所有素数
const int n = 100;

bool isPrime[n + 1] = {true};

int prime[n];

int index = 0;

for(int i = 2; i <= n; i++) {
    // 某个数为素数
    if(isPrime[i]){
        prime[index++] = i;
    }
    for(int j = 0; j <= index && i * prime[j] <= n; j++) {
        isPrime[i * prime[j]] = false;
        // 若i是prime[j]的倍数, 当i = k * prime[j+1]时会重复
        if (i % prime[j] == 0) {
            break;
        }
    }
}