导数

基本初等函数导数推导 高等数学微积分—-教你如何简单地推导求导公式(一)

定义

函数在某一点的导数是指函数在这该点附近变化率

• 设函数$f(x)$ 在 $x_0$ 附近有定义

对应自变量改变量$\Delta x$

有函数改变量 $\Delta y = f(x_0 + \Delta x) - f(x_0)$

若极限 $\lim\limits_{x\rightarrow 0}\frac{\Delta y}{\Delta x}$ 存在

则称该极限为$f(x)$ 在 $x_0$ 处导数, 记作 $f^{‘}(x_0)$

引理

常数函数导数处处为零

• 设 $f(x) = C$

$f^{‘}(x) = \lim\limits_{x\rightarrow 0}\frac{f(x + \Delta x) - f(x)}{\Delta x}$

$= \lim\limits_{x\rightarrow 0}\frac{C - C}{\Delta x}$

$= \lim\limits_{x\rightarrow 0}\frac{0}{\Delta x}$

$= 0$

图形化

$f(x) = x^2$

对于该公式可以表示一个边长为 $x$ 正方形面积公式

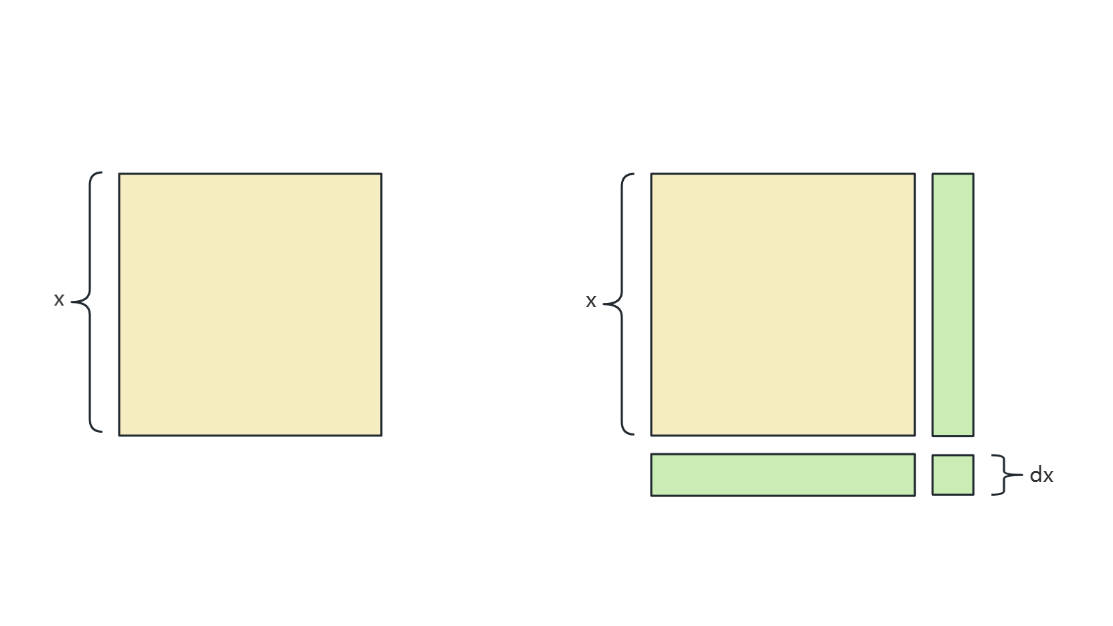
从导数层面理解, 设当变量 $x$ 增加 $dx$ 时, $f(x)$ 所增加为面积 $df$

$df$ = 两个长为 $x$, 宽为 $dx$ 长方形面积 +一个边长为 $dx$ 正方形面积

既有 $df = 2xdx + (dx)^2$

当 $dx $无限趋近于 $0$ 时, $(dx)^2$ 小到可被忽略, 则有

$df = 2xdx$ => $\frac{df}{dx} = 2x$

所以$f^{‘}(x) = 2x$